In market research, it is often required to assess how to reach the largest number of potential customers.
This need can be address by adopting a TURF (Total Unduplicated Reach and Frequency) model which helps to identify the optimal combination(s) of product characteristics or communication messages, i.e., those that will have the greatest reach across the respondent base.
TURF was originally developed for analysis of media campaigns, to selecting media vehicles so as to minimize the extent of overlap of the audiences reached. TURF has since been expanded to apply to product and service development and is now used to answer questions such as:
- What would be the impact on our market share if we add a new product line to our offering?
- What combination of messages would allow us to reach the largest possible number of customers?
- What combination of channels should we use for our ads to reach the widest possible audience?
Typically, a TURF analysis allows to:
- estimate the reach of any combination of items;
- identify the combinations of items with the largest reach (one can test combination of various sizes, e.g., combination of 3 items), i.e., the optimal combinations;
- take into account the cost of individual items to identify optimal combinations within a predefined total cost range;
- estimate the incremental value in reach when adding an item to a particular combination;
- assess to which extent the items are mutually exclusively or whether there is an large overlap among them;
- force one or more items into the optimal combinations.
Typical TURF project example: Company X has a large database of customers describing the communication channel that each customer is exposed or is not exposed to (e.g., journal X, podcast Y. forum Z, etc). Company X needs to identify which combination of, say 4, channels allows reaching the largest number of customers, so that resources can be focused on such channels.
Typically, a customer is considered to be reached by a given set of channels if he or she is exposed to at least one of the channels in the set (i.e., depth of the reach = 1). However, more restrictive definitions can be used, i.e., the depth of the reach could be higher than 1. For instance, if we choose a depth of 2, then a customer is considered to be reached by a given set of channels if he or she is exposed to at least two of the channels in the set.
It is also possible to consider various levels of exposure (not just exposed / not exposed) to the channels, possibly reflecting the exposure (or purchase) frequency. In this case, a respondent is considered to be reached by a given set of channels if he or she has an overall exposure (across the various channels in the set) equal or larger than a prespecified level.
When running TURF, one needs to decide whether to weight the respondents, the items, or both:
- respondents weights are computed when one wants to adjust for discrepancies between the sample distribution and the population distribution.. In this case, some respondents are assigned a larger weight and some other respondents a lower weight;
- usually, each item analysed in a TURF model has a weight of one, which means that each item has the same contribution towards the reach score. It might be required, however, to assign a larger weight to some items, for instance to reflect differences in cost or in feasibility of the items.
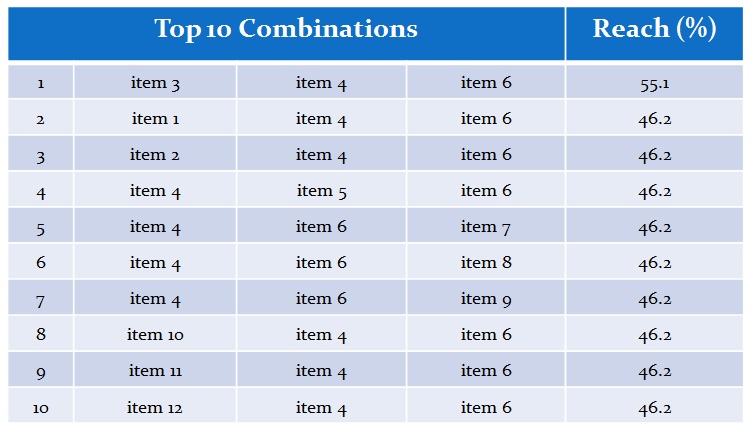
TURF analysis typically assesses all possible combinations of 2-6 channels (referred to as TURF items) and for each combination the reach is computed. In a typical deliverable, the TURF algorithm lists all possible combinations of items (or the top 10, 100, etc.) sorted by their reach value in descending order.
In the example below, the table lists the 10 combinations of 3 items with the largest reach.
The TURF algorithm should be computationally efficient as the number of combinations to be assessed increases exponentially with the number of items to be considered:
For instance, assuming there are 40 TURF items to be considered, the algorithm would need to assess:
- C(40,2) = 780 combinations of 2 items
- C(40,3) = 9,880 combinations of 3 items
- C(40,4) = 91,390 combinations of 4 items
- C(40,5) = 658,008 combinations of 5 items
- C(40,6) = 3,838,380 combinations of 6 items
- …
- C(40,10) = 847,660,528 combinations of 10 items
The functions turf.analysis available in R-sw Discriminant allows running TURF analysis. The algorithm is very flexible, allowing for various depths of analysis, a large number of respondents and TURF items, combinations of items of various sizes, item cost, item forced into the model, and, if required, for weights to be applied to both respondents and items.
